গড় নির্ণয়ের সূত্র ও কৌশল

সহজ ও সংক্ষিপ্ত পদ্ধতিতে গাণিতিক গড় নির্ণয়

---

• গড় কি বা গড় কাকে বলে
• সংক্ষিপ্ত পদ্ধতিতে গড় নির্ণয়ের সূত্র
• সহজ ও মজার পদ্ধতিতে গড় নির্ণয়
• গাণিতিক গড় নির্ণয়
• গড় নির্ণয়ের সূত্র
• গড় নির্ণয়ের পদ্ধতি ও প্রকারভেদ

---

গড় নির্ণয়ের সূত্র ও পদ্ধতি

বীজগনিত বা পাটিগণিতে পরিসংখ্যান বা Statistics অধ্যায়ে বা তথ্য উপাত্য অধ্যায়ে গড় বা গাণিতিক গড় কি, কাকে বলে বা গড় করার নিয়ম সম্পর্কে ভয় ও বিভ্রান্তি লক্ষ্য করা যায়। কিভাবে সমাধান করবো, গড় ও গাণিতিক গড় নির্ণয়ের পদ্ধতি কি একই? সংক্ষিপ্ত ও সহজ পদ্ধতিতে কিভাবে গড় নির্ণয় করতে হয়? এমন নানান প্রশ্ন দেখা দেয় ছাত্র ছাত্রীদের মনে। ৫ম, ৬ষ্ঠ, ৭ম, ৮ম, ৯ম, ১০ম থেকে শুরু করে এইচএসসি বা ১১-১২ শ্রেণি এমনকি অনার্স মাস্টার্স লেভেলেও গড় বিষয়টি খুবি গুরুত্বপূর্ণ। আজকের আলোচনা গড় সম্পর্কে বিস্তারিত। সহজ, সংক্ষিপ্ত ও কৌশলগত মজার পদ্ধতি প্রয়োগ করে বিষয়টি এমন ভাবে উপস্থাপন করা হয়েছে, আশাকরি সকলে গড় সম্পর্কে না বুঝে আর থাকবো না।

গড় কি বা কাকে বলেঃ

গড় কি বা গড় কাকে বলে অর্থাৎ গড় মানে কি, এসম্পর্কে বুঝতে গেলে একটি গল্প না বললেই নয়। মনে করো, তিন সাইজের ৩ টি ঘোড়া নিয়ে তুমি ঘোড়ার ব্যাবসা শুরু করলে। তোমার ইচ্ছা, লাল রং এর বড় ঘোড়াটি ৫০০০০ টাকায় বিক্রি করবে, সাদা রং এর মাঝারি সাইজের ঘোড়াটি বিক্রি করবে ৩০০০০ টাকায় এবং ছোট্ট কালো রং এর বাচ্চা ঘোড়াটি বিক্রি করবে ১০০০০ টাকায়। যদি তিনটি ঘোড়া এই দামে বিক্রি করো তবে তুমি মোট ৫০০০০+৩০০০০+১০০০০=৯০০০০ টাকা পাবে। অর্থাৎ তোমার তিনটি ঘোড়া বিক্রি করে ৯০০০০ টাকা পেলেই তুমি হ্যাপি বা সন্তুষ্ট। এখন, একটি লোক ঘোড়া কিনতে তোমার কাছে এল। সে বললো ভাই তোমার তিনটি ঘোড়ায় আমি নেবো, বড় ছোটো বুঝি না, রং চোং বুঝি না। আমি ছোট বড় সকল ঘোড়া একই দামে কিনবো এবং প্রতিটি ঘোড়ার দাম দিবো ৩০০০০ টাকা করে। তুমি বিষয়টি নিয়ে ভাবলে। তোমার তিনটি ঘোড়া বিক্রি করে ৯০০০০ টাকা প্রয়োজন ছিল। আর এই ক্রেতা প্রতিটি ঘোড়া যদি ৩০০০০ টাকা করে ক্রয় করে তবুও তোমার কোনো লোকসান হবে না। কারণ লাল রং এর বড় ঘোড়াটি যদি ৩০০০০ টাকায় বিক্রি করো তবে সাদা রং এর মাঝারি টিও ৩০০০০ টাকা বিক্রি করতে পারছো এমনকি ছোট্ট কালো ঘোড়াটিও বিক্রি করতে পারছো ৩০০০০ টাকায়। সুতারং ৩০০০০+৩০০০০+৩০০০০=৯০০০০ টাকা তুমি পেয়ে যাবে ফলে কোনো লোকসান হবে না। এবার উদাহরণ বা ঘোড়ার গল্পটি লক্ষ্য করো। ছোট বড় প্রতিটি ঘোড়া ৩০০০০ টাকা বিক্রি করলে যেহেতু যত টাকায় মোট বিক্রি করতে চেয়েছিলে সেই দাম পাচ্ছ সুতারং এই ৩০০০০ টাকাই হলো তিনটি ঘোড়ার গড় দাম! অর্থাৎ কিছু এলো মেলো তথ্য যদি এলো মেলো ভাবে না ধরে সমান হারে ধরা হয় তবে সেই সমান বা সাধারণ তথ্যই হলো গড় তথ্য বা গড়। ইংরেজীতে গড়কে Average বা Mean বা মীন বলে। গড় বা গাণিতিক গড় নির্ণয়ের পদ্ধতি কে x̄ Theory বা X বার থিওরি বলা হয়ে থাকে।

গড়ের প্রকারভেদঃ

গড়কে নানান ভাবে প্রকরণ করা যেতে পারে। বিশ্লেষণ ও ক্ষেত্রগত দিক দিয়ে গড় কে ৩ টি ভাগে ভাগ করা হয়ে থাকে। অর্থাৎ গড় ৩ প্রকার। যথা-

• ১. গাণিতিক গড় বা Arithmetic Mean (এটি মূলত পাঠ্য বইয়ে থাকা গড়, যা নিয়ে এখানে বিস্তারিত আলোচনা হবে) 
• ২. গুণিতক গড় বা Geometric Mean (আনুপাতিক হিসাব, পরিবর্তন বা শতকরা হিসাবের গড় বের করতে ব্যাবসা প্রতিষ্ঠানে এই পদ্ধতিতে গড় বের করা হয়, নিম্ন শ্রেণীর পাঠ্য বইয়ে এ পদ্ধতি না থাকায় এ বিষয়ে এখানে আলোচনা করা হবে না) 
• ৩. তরঙ্গ গড় বা Harmonic Mean (শেয়ার প্রতি গড় আয়, টাকা প্রতি গড় আয় বা এমন ক্ষেত্রে এই পদ্ধতিতে গড় নির্ণয় করা হয়ে থাকে, নিম্ন শ্রেণীর পাঠ্য বইয়ে এ পদ্ধতি না থাকায় এখানে আলোচনা করা হবে না)

 

গাণিতিক গড় কি বা কাকে বলেঃ

গড় বলতে গাণিতিক গড়কেই বোঝায়। ৫ম, ৬ষ্ঠ, ৭ম, ৮ম, ৯ম, ১০ম বা উচ্চ শ্রেণীতে আমরা পরিসংখ্যান বা তথ্য উপাত্ত অধ্যায়ে যে গড় করি তা মূলত গাণিতিক গড়। গণিতের সূত্র প্রয়োগ করে গড় নির্ণয় করাকে গাণিতিক গড় বলে। অর্থাৎ এটা স্পষ্ট যে আমরা নিজ নিজ শ্রেণীতে যতো প্রকার গড় নির্ণয় করি তার সকল পদ্ধতি কেই গাণিতিক গড় বলে। তাই পরীক্ষায় গাণিতিক গড় করতে বললে বিশেষ কোনো পদ্ধতিতে গড় করতে হবে না। তুমি যতো প্রকারের গড় করেছো বা যে যে সূত্র ব্যবহার করে যে যে পদ্ধতিতে গড় নির্ণয় করেছো তার সবি গাণিতিক গড় বা গড়। ইংরেজীতে গড় বা গাণিতিক গড়কে Arithmetic mean বলা হয়ে থাকে।

এক নজরে গড় নির্ণয়ের পদ্ধতি সমূহঃ

নিচের চিত্রে ছক বা চার্ট আকারে গড় নির্ণয়ের পদ্ধতি সমূহ তুলেধরা হলো। আশাকরি চার্ট বা ছকটি গাণিতিক গড় বা গড় নির্নয়ের জন্য খুবি সহায়ক হবে-

গড় নির্ণয়ের ছক বা চার্ট

গড় নির্ণয়ের সূত্রঃ

গড় বলতে আমরা গাণিতিক গড়কে বুঝি। তাই বই এর সকল সূত্র বা পদ্ধতিই গাণিতিক গড় বা গড়। অপর দিকে তথ্য উপাত্ত বই এ ২ ভাবে দেওয়া থাকে, যথা-

• ১. ছক বিহীন তথ্য 
• ২. ছকে থাকা তথ্য

নিম্নে ছক বিহীন ও ছকে থাকা তথ্যের গড় বা গাণিতিক গড় নির্ণয়ের সূত্র বা পদ্ধতি সহজ ভাবে তুলে ধরা হলো।

ছক বিহীন তথ্যের গড় নির্ণয়ের সূত্রঃ

ছক বিহীন তথ্যের গড় বা গাণিতিক গড় নির্ণয়ের সূত্রটি হলো-

গড় বা গাণিতিক গড় = রাশি সমষ্টি ÷ রাশি সংখ্যা।

এখানে রাশিগুলোর সমষ্টি বলতে তথ্য উপাত্তের সমষ্টিকে বোঝানো হয়েছে এবং রাশি সংখ্যা বলতে তথ্য উপাত্তে থাকা গণসংখ্যাকে বোঝানো হয়েছে।

উদাহরণঃ

৩০, ১৫, ১০, ৩৫, ১০ তথ্য বা ছক বিহীন তথ্য গুলোর গড় বা গাণিতিক গড় নির্ণয় কর।

সমাধানঃ

প্রদত্ত তত্যের, রাশি সমষ্টি = ৩০ + ১৫ + ১০ + ৩৫ + ১০ = ১০০ এবং রাশি সংখ্যা = ৫ টি অতএব,

গড় বা গাণিতিক গড়=১০০÷৫=২০

ছকে থাকা তথ্যের গড় নির্ণয়ের সূত্রঃ

ছকে থাকা তথ্য সাধারন্ত দুটি ভাবে থাকে। যথা-

• ১. গুরুত্ব যুক্ত ছকে থাকা তথ্যের গড় নির্ণয় 
• ২. শ্রেণী যুক্ত ছকে থাকা তথ্যের গড় নির্ণয়

গুরুত্ব যুক্ত ছকে থাকা তথ্যের গড় নির্ণয়ঃ

গুরুত্ব যুক্ত ছকে থাকা তথ্যের গড় বা গাণিতিক গড় নির্ণয় করতে গেলে গুরুত্ব যুক্ত তথ্য সম্পর্কে আমাদের ধারনার্জন প্রয়োজন। তথ্য গুলো শ্রেণী ব্যাপ্তিতে বিভক্ত না করে যদি ছকে উপস্থাপন করা হয় তখন তাকে গুরুত্ব যুক্ত তথ্য ছক বা সারণী বলে। গণসংখ্যা সারণী থেকে গুরুত্ব যুক্ত তথ্যের গড় বা গাণিতিক গড় নির্ণয়ের জন্য অতিরিক্ত একটি ঘর কাটতে হয়। ঘরটির নাম, তথ্য x গণসংখ্যা। গুরুত্ব যুক্ত তথ্যের গড় বা গাণিতিক গড় নির্ণয়ের সূত্র হলো-

গড় বা গাণিতিক গড় = (তথ্য x গনসংখ্যর সমষ্টি) ÷ গনসংখ্যা।

নিচে ছবিতে সূত্রটি সুন্দর ভাবে তুলে ধরা হলো-

গুরুত্ব যুক্ত তথ্যের গড় সূত্র

উদাহরণঃ

নিম্নের ছক থেকে গুরুত্ব যুক্ত তথ্যের গড় নির্ণয় করো-

টাকার পরিমাণ	গণসংখ্যা
১০	২
১৫	১
৩০	১
৩৫	১

সমাধানঃ

গুরুত্ব যুক্ত তথ্যের গড় নির্ণয়ের জন্য সারণী তৈরী করা হলো-

টাকার পরিমাণ (xi)	গণসংখ্যা (wi)	টাকার পরিমাণ x গণসংখ্যা (xi.wi)
১০	২	২০
১৫	১	১৫
৩০	১	৩০
৩৫	১	৩৫
-	মোট=৫	সমষ্টি=১০০

অতএব,

গড় বা গাণিতিক গড়= ১০০÷৫=২০

শ্রেণী যুক্ত ছকে থাকা তথ্যের গড় নির্ণয়ঃ

শ্রেণী যুক্ত বলতে শ্রেণী ব্যাপ্তি আছে এমন তথ্য উপাত্তকে বোঝানো হয়েছে। ৫-১০ বা ১৯-২০ এমন ভাবে শ্রেণীতে তথ্য থাকলে তাকে শ্রেণী যুক্ত তথ্য বলে। শ্রেণী যুক্ত তথ্যের গড় নির্ণয়ের ২ টি পদ্ধতি রয়েছে। যথা-

• ১. সাধারণ পদ্ধতিতে গড় নির্ণয় (শ্রেণী যুক্ত ছকে থাকা তথ্য) 
• ২. সংক্ষিপ্ত বা সহজ পদ্ধতিতে গড় নির্ণয় (শ্রেণী যুক্ত ছকে থাকা তথ্য)

 

সাধারণ পদ্ধতিতে গড় নির্ণয়ের সূত্র - ছকে থাকা শ্রেণী যুক্ত তথ্যঃ

ছকে থাকা শ্রেণী যুক্ত তথ্যের গড় নির্ণয়ের সূত্র হলো-

গড় বা গাণিতিক গড় = (গণসংখ্যা x মধ্যমানের সমষ্টি) ÷ গণসংখ্যা

অন্যভাবে বলা যায়, গড় বা গাণিতিক গড়কে x̄, গণসংখ্যাকে fi, গণসংখ্যার সমষ্টিকে n, মধ্যমানকে xi ধরলে, গণসংখ্যা গুণ মধ্যমান হবে fi.xi এবং গণসংখ্যা গুণ মধ্যমানের সমষ্টি হবে ∑fi.xi সুতারং গড় নির্ণয়ের সূত্রটি হবে,

গড় বা গাণিতিক গড়, x̄=(∑fi.xi)÷n

নিচে ছবিতে সূত্রটি সুন্দর ভাবে তুলে ধরা হলো-

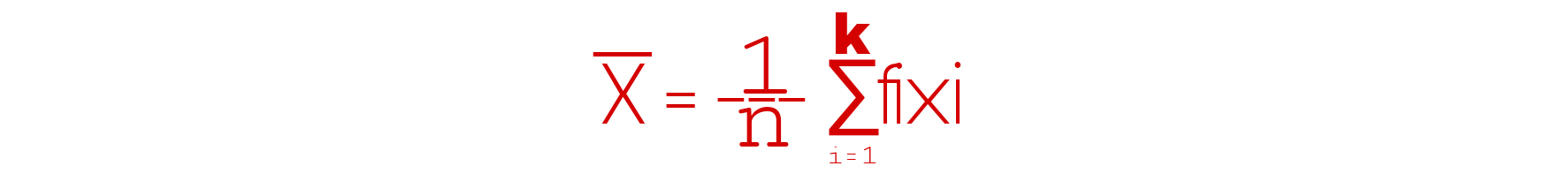শ্রেণী বিন্যাসকৃত তথ্যের গড় নির্ণয় সূত্র

শ্রেণী যুক্ত তথ্যের সাধারণ পদ্ধতিতে গড় নির্ণয়ের জন্যে ছকে অতিরিক্ত দুটি ঘর কাটতে হয়। অতিরিক্ত ঘর দুটি হলো-

• ১. শ্রেণীর মধ্যমান বা xi 
• ২. মধ্যমান x গণসংখ্যা বা fi.xi

নিম্নে উদাহরণের সাহায্যে বিষয়টি সহজ ভাবে বোঝানো হলো।

উদাহরণঃ

প্রদত্ত তথ্যের গড় বা গাণিতিক গড় নির্ণয় করঃ

শ্রেণী ব্যাপ্তি	গণসংখ্যা
১১-২০	২
২১-৩০	১
৩১-৪০	১
৪১-৫০	১

সমাধানঃ

গড় বা গাণিতিক গড় নির্ণয়ের জন্য (সাধারণ পদ্ধতি) ছক তৈরি করা হলো-

শ্রেণী ব্যাপ্তি	শ্রেণীর মধ্যমান (xi)	গণসংখ্যা (fi)	শ্রেণীর মধ্যমান x গণসংখ্যা (fi.xi)
১১-২০	১৫.৫	২	৩১
২১-৩০	২৫.৫	১	২৫.৫
৩১-৪০	৩৫.৫	১	৩৫.৫
৪১-৫০	৪৫.৫	১	৪৫.৫
------	-----	n=৫	∑fi.xi=১৩৭.৫

অতএব,

গড় বা গাণিতিক গড়, 

x̄=(∑fi.xi)÷n বা, ১৩৭.৫ ÷ ৫ বা, ২৭.৫

সংক্ষিপ্ত বা সহজ পদ্ধতিতে গড় নির্ণয়ের সূত্র - ছকে থাকা শ্রেণী যুক্ত তথ্যঃ

সংক্ষিপ্ত বা সহজ পদ্ধতিতে গড় বা গাণিতিক গড় নির্ণয় করতে গেলে ছকে অতিরিক্ত ৩ টি ঘর বেশি কাটতে হয়। ঘর গুলো হলো-

• ১. মধ্যমান বা xi 
• ২. ধাপ বিচ্যুতি বা ui 
• ৩. গণসংখ্যা x ধাপ বিচ্যুতি বা fi.ui

গড় বা গাণিতিক গড়কে x̄, গণসংখ্যাকে fi, শ্রেণী ব্যাপ্তি কে h, গণসংখ্যার সমষ্টিকে n, মধ্যমানকে xi, অনুমিত শ্রেণীর মধ্যমানকে a, ধাপ বিচ্যুতি কে ui ধরলে গণসংখ্যা গুণ ধাপ বিচ্যুতি হবে fi.ui এবং গণসংখ্যা গুণ ধাপ বিচ্যুতির সমষ্টি হবে ∑fi.ui সুতারং সংক্ষিপ্ত বা সহজ পদ্ধতিতে গড় নির্ণয়ের সূত্রটি হবে-

গড় বা গাণিতিক গড় = অনুমিত শ্রেণীর মধ্যমান + (গণসংখ্যা গুণ ধাপ বিচ্যুতির সমষ্টি ÷ গণসংখ্যা) x শ্রেণী ব্যাপ্তি।

অর্থাৎ-

x̄=a+(∑fi.ui÷n).h

নিচে ছবিতে সূত্রটি সুন্দর ভাবে তুলে ধরা হলো-

সংক্ষিপ্ত পদ্ধতিতে গড় নির্ণয় সুত্র

এখানে, ধাপ বিচ্যুতি নির্ণয়ের জন্যে ছকের মাঝামাঝি একটি ঘরে শূন্য বা ০ ধরতে হয়। ঘর সংখ্যা জোড় হলে মাঝে দুটি ঘর থাকে সে ক্ষেত্রে যে দুটি ঘর মাঝে পড়ে তার নিচের টি তে ০ ধরতে হয়। এই শূন্য ধরা শ্রেণী বা লাইন টি হলো অনুমিত শ্রেণী। যে ঘরে ০ ধরা হবে তার আগের ঘরে -১, তার আগের ঘরে -২, তার আগের ঘরে -৩ এভাবে ঘর গুলো পূর্ণ করতে হবে। আবার যে ঘরে ০ ধরা হবে তার নিচের ঘরে +১, তার নিচের ঘরে +২, তার নিচের ঘরে +৩, তার নিচের ঘরে +৪ এভাবে পূর্ণ করতে হবে। এভাবে ধাপ বিচ্যুতি ঘর বা ui ঘর পূর্ণ করার পর যে ঘরে ০ ধরা হয়েছে সেই লাইনে বাম দিকে মধ্যমানের ঘরে যে মান থাকবে সেই মান হবে অনুমিত শ্রেণীর মধ্যমান বা a এর মান।

নিম্নে উদাহরণের মাধ্যমে সহজ বা সংক্ষিপ্ত পদ্ধতিতে গড় বা গাণিতিক গড় নির্ণয়ের সূত্র ও পদ্ধতি সম্পর্কে বোঝানো হলো।

উদাহরণঃ

প্রদত্ত তথ্যের সহজ বা সংক্ষিপ্ত পদ্ধতিতে গড় বা গাণিতিক গড় নির্ণয় করঃ

শ্রেণী ব্যাপ্তি	গণসংখ্যা
১১-২০	২
২১-৩০	১
৩১-৪০	১
৪১-৫০	১

সমাধানঃ সহজ বা সংক্ষিপ্ত পদ্ধতিতে গড় বা গাণিতিক গড় নির্ণয়ের জন্য নিম্নে ছক তৈরি করা হলো-

শ্রেণী ব্যাপ্তি	শ্রেণীর মধ্যমান (xi)	গণসংখ্যা (fi)	ধাপ বিচ্যুতি (ui)	গণসংখ্যা x ধাপ বিচ্যুতি (fi.ui)
১১-২০	১৫.৫	২	-২	-৪
২১-৩০	২৫.৫	১	-১	-১
৩১-৪০	৩৫.৫=a	১	০	০
৪১-৫০	৪৫.৫	১	+১	১
------	------	n=৫	---	∑fi.ui=-৪

এখানে অনুমিত শ্রেণী ৩১-৪০, কারণ এই শ্রেণীতেই বিচ্যুতি মান ০ ধরা হয়েছে, সুতারং এই শ্রেণীর মধ্যমান বা অনুমিত শ্রেণীর মধ্যমান a=৩৫.৫ এবং ৩১থেকে ৪০ পর্যন্ত ১০ টি সংখ্যা আছে, সুতারং শ্রেণী ব্যাপ্তি h=১০

অতএব, 

গড় বা গাণিতিক গড় x̄

= a+(∑fi.ui÷n).h

= ৩৫.৫ + (-৪÷৫) ১০ 

= ৩৫.৫ + (-০.৮)১০

= ৩৫.৫ + (-৮)

= ৩৫.৫ - ৮

= ২৭.৫

বিশেষ দ্রষ্টব্যঃ ∑ এটি স্যামেশন এর চিহ্ন, যার অর্থ সমষ্টি বা যোগফল। ∑f বলতে বোঝায় f এর সমষ্টি আর একে, স্যামেশন অফ f, এভাবে পড়া হয়।

উৎপাদক নির্ণয়ের মজার ও সহজ সূত্র শিখতে এখানে ক্লিক করুন>>>

---

শুভকামনায় 

কে-মাহমুদ

৮-১-২০২১